FraktaliUvod

Gledajući prirodu, možda ste primijetili zamršene biljke poput ovih:

Ovo Paprat sastoji se od mnogo malih listova koji se granaju sa većeg.

Ova Romanesco brokula sastoji se od manjih koji se spiraliraju oko većeg.

U početku se to čine kao vrlo složeni oblici, ali kada pogledate bliže, primijetit ćete da oboje slijede relativno jednostavan obrazac: svi pojedinačni dijelovi biljaka izgledaju potpuno isto kao i cijeli biljka, samo manja. Isti se obrazac ponavlja iznova i iznova, na manjim mjerilima.

U matematici ovo svojstvo nazivamo sličnošću, a oblici koji ga imaju nazivaju se fraktalima. Oni su neki od najljepših i najbizarnijih predmeta u čitavoj matematici.

Da bismo stvorili vlastite fraktale, moramo početi s jednostavnim uzorkom, a zatim ga ponavljati iznova i iznova, na manjim mjerilima.

Jedan od najjednostavnijih obrazaca mogao bi biti linijski segment, s još dva segmenta koji se granaju s jednog kraja. Ako ponovimo ovaj uzorak, oba ova plava segmenta također će imati još dvije grane na svojim krajevima.

Možete pomicati plave točke za promjenu duljine i kuta svih grana. Zatim povećajte broj ponavljanja pomoću klizača u nastavku.

Ovisno o položaju grana, možete napraviti potpuno drugačije obrasce - izgledajući poput gore, ili . Što još možete pronaći?

Još jedan poznati fraktal je Sierpinski trokut. U ovom slučaju započinjemo velikim, jednakostraničnim trokutom, a zatim više puta izrezujemo manje trokut od preostalih dijelova.

Primijetite kako se konačni oblik sastoji od tri identične kopije samog sebe, a svaku od njih čine još manje kopije cijelog trokuta! Možete nastaviti zumirati u trokut zauvijek, a obrasci i oblici uvijek će se ponavljati.

Biljke na početku ovog poglavlja izgledaju baš poput fraktala, ali očigledno je nemoguće stvoriti istinske fraktale u stvarnom životu. Ako stalno i iznova ponavljamo isti obrazac, sve manji i manji, na kraju bismo stigli do stanica, molekula ili atoma koji se više ne mogu podijeliti.

Međutim, koristeći matematiku, možemo razmišljati o svojstvima koja bi stvarni fraktali "imali" - a to su vrlo iznenađujuća ...

Fraktalne dimenzije

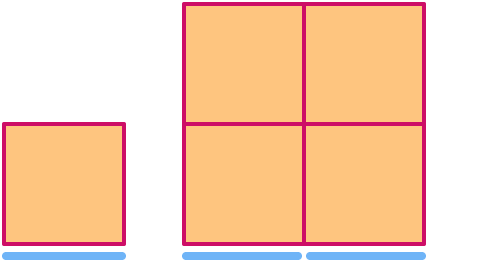
Prvo, razmislimo o dimenziji fraktala. Crta ima dimenziju . Kada ga skalirate za faktor 2, njegova duljina se povećava za faktor 21=2. Očito!

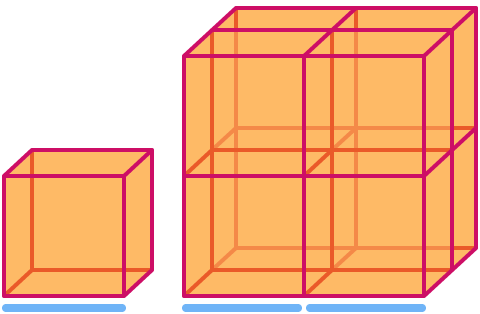
Kvadrat ima dimenziju . Kada ga skalirate za faktor 2, njegova površina se povećava za faktor 22=

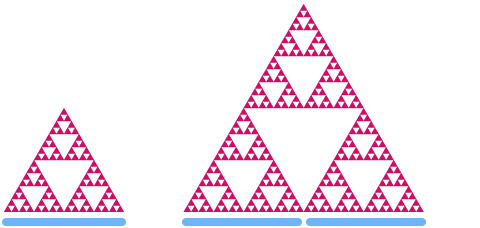
Kocka ima dimenziju . Kada ga skalirate za faktor 2, njegov se volumen povećava za faktor 23= Primjetite da je veća kocka na slici sastoji se od 8 primjeraka manjeg!

Pogledajmo sada Sierpinski trokut. Ako ga skaliramo s faktorom 2, možete vidjeti da se "područje" povećava za faktor .

Recimo da je d dimenzija Sierpinskog trokuta. Koristeći isti obrazac kao gore, dobivamo 2d=3. Drugim riječima, d = ≈ 1.585 ...

Ali pričekajte ... kako nešto može imati dimenziju koja nije cijeli broj? Čini se nemogućim, ali ovo je samo jedno od čudnih svojstava fraktala. U stvari, to je ono što daje fraktalima svoje ime: oni imaju frakcijsku dimenziju.

Svakom iteracijom uklanjamo dio područja Sierpinskog trokuta. Kad bismo to mogli raditi beskonačno mnogo puta, zapravo ne bi ostalo područje: to je razlog zašto je Sierpinski trokut nešto između dvodimenzionalnog područja i jednodimenzionalne crte.

Iako su mnogi fraktalni slični, bolja definicija je da su fraktalni oblici koji imaju ne-cijelu dimenziju.

Kochova pahulja

U prirodi postoji mnogo oblika koji izgledaju poput fraktala. Neke biljke smo već vidjeli na početku ovog poglavlja. Drugi sjajni primjeri su snježne pahulje i ledeni kristali:

Da bismo stvorili vlastitu fraktalnu pahuljicu, još jednom moramo pronaći jednostavan postupak koji možemo primjenjivati iznova i iznova.

Kao i Sierpinski trokut, započnimo s jednim, jednakostraničnim trokutom. No, umjesto uklanjanja manjih trokuta na svakom koraku, zbrajamo manje trokut uz rub. Dužina stranice svakog trokuta je trokuta u prethodnom koraku.

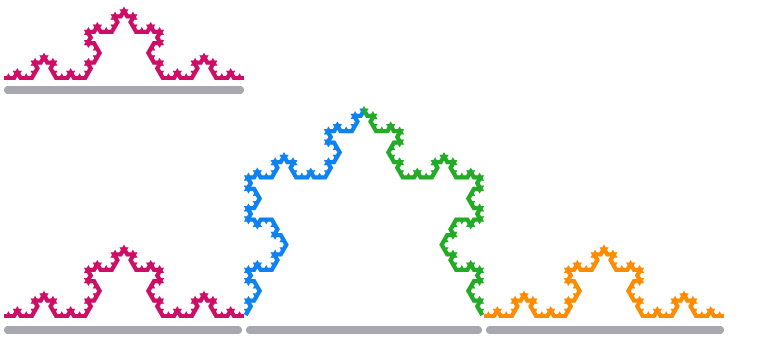
Rezultirajući oblik naziva se Kochova pahulja, nazvana po švedskom matematičaru Helge von Koch. Još jednom primijetite da mali presjeci ruba snježne pahulje izgledaju potpuno isto kao veći odjeljci.

Kada pomaknemo jedan rubni segment Kochove pahulje sa faktorom 3, njegova duljina .

Koristeći isti odnos dimenzija i faktora razmjera kao gore, dobit ćemo jednadžbu . To znači da je dimenzija Kochove pahulje d=log34≈1.262.

Područje

Stvaranje Kochovih pahuljica gotovo je poput rekurzivnog slijeda: znamo početni oblik (trokut) i znamo kako prijeći iz jednog termina u drugi (dodavanjem više trouglova na svaki rub):

novi trokut

Nakon prve iteracije, broj novih dodanih trokuta povećava se za faktor na svakom koraku. Istovremeno, površina ovih novih trokuta smanjuje se za faktor na svakom koraku.

Recimo da prvi trokut ima površinu 1. Tada je ukupna površina sljedeća tri trougla 3×19=13. Sljedeći koraci čine , sa zajedničkim omjerom .

Koristeći formulu za zbroj beskonačnih geometrijskih serija, možemo izračunati da je ukupna površina Kochove pahulje

A=1+13×1=85=1.6.

Perimetar

Također možemo pokušati izračunati perimetar Koch snježne pahulje. Kao što smo već vidjeli, duljina perimetra se mijenja za faktor na svakom koraku.

To znači da, opet, imamo geometrijski niz, ali u ovom slučaju, . To znači da je perimetar Kochove snježne pahulje zapravo beskrajno dugačak!

Ako se ovo čini kontraintuitivno, sjetite se da pomnožimo obod sa 43 na svakom koraku, i to radimo beskonačno mnogo puta.

Gotovo je nezamislivo da možete imati oblik s konačnim područjem i obodom beskonačno - ali ovo je samo jedno od mnogih neočekivanih svojstava fraktala.

Možete li smisliti bilo koji drugi način stvaranja vlastitih fraktala?

"Moja duša se spiralira na smrznutim fraktalima svuda okolo ..."

Menger spužva

Fraktali ne moraju biti "ravni", poput mnogih gore navedenih primjera. Jedan od najpoznatijih fraktala koji izgleda trodimenzionalno je Menger spužva, nazvan po matematičaru Karlu Mengeru koji ga je prvi opisao 1926. godine.

Počinjemo s čvrstom kockom i opetovano izbušimo sve manje i manje rupe na njenim stranama. Svaka nova iteracija rupa ima širinu prethodne iteracije rupa.

Kocka 3×3×3 sastoji se od 27 manjih kockica, ali ovdje smo ih uklonili. Mengerova spužva se sastoji od samih kopija koje su 3 puta manje.

Sada možemo pokušati izračunati dimenziju d Mengerove spužve baš kao što smo to radili za Kochovu pahuljicu gore. U ovom slučaju dobili smo 3d=20, ili d=log320≈2.727.

Ako zamislite da izrezujete sve više i više rupa, beskonačno mnogo puta, ne bi preostao stvarni volumen. Zbog toga je kocka "ne baš" trodimenzionalna!

Fraktalne obale

Jedna od ključnih karakteristika svih fraktala koje smo do sada vidjeli jest da možete "zumirati" zauvijek i uvijek pronaći nove obrasce. Oko 1920. godine britanski matematičar Lewis Fry Richardson shvatio je da isto vrijedi i za granicu ili obalu mnogih zemalja.

Počinjete s osnovnim oblikom zemlje i, kako povećavate, dodajete riječne dotoke, uvale i ušća, zatim pojedinačne litice, stijene, šljunak i tako dalje:

Ovo je značajan problem kada pokušavate izračunati duljinu granice neke zemlje - kako odlučiti koliko želite zumirati i koje čvorove i krajeve uključiti?

Jedan od načina na koji bismo mogli izmjeriti dužinu britanske obale, je naprimjer uzeti dugog vladara, prošetati njegovim plažama i zatim zbrojiti sve udaljenosti.

Ako je vladar dugačak ${rulers[index]} km, moramo ga upotrijebiti ${count} puta, pa ćemo dobiti ukupnu obalu ${count} × ${rulers[index]} = ${count * rulers[index]} km.

Samo možemo nastaviti, s manjim i manjim vladarima, i svaki put bi naš rezultat u duljini obale postajao malo duži. Kao i prije Kochove pahulje, čini se da je britanska obala beskonačno duga! To se često naziva paradoks obale.

Nekoliko desetljeća kasnije, matematičar Benoit Mandelbrot našao se na Richardson-ovom radu u odbačenoj knjižničarskoj knjizi, radeći u IBM-u. Prepoznao je njegov značaj, kao i povezanost s novijim istraživanjima fraktala i dimenzija.

Obala Britanije sigurno "izgleda" fraktalno, ali nije sam sebi slična, kao ostali fraktali koje smo vidjeli prije. Da bismo pronašli njegovu veličinu, možemo je nacrtati na rešetki i brojati broj ćelija s kojima se presijeca.

U početku postoje 88 stanice koje se presijecaju. Ako skaliramo obalu s faktorom 2, tu je 197 stanica koje se presijecaju - više nego dvostruko više!

Veličina obalne crte povećala se za faktor 19788. Kao i prije, to znači da je dimenzija obale

d=log219788≈1.16

Ako ponovimo ovo sa većim mrežama, otkrili bismo da je dimenzija britanske obale zapravo otprilike 1,21. Mandelbrot je shvatio da je ta fraktalna dimenzija ujedno i mjera hrapavosti oblika oblika - novi koncept, za koji je pronašao važne primjene u mnogim drugim područjima matematike i znanosti.

Još fraktala iz prirode i tehnologije

Iako se istinski fraktali nikada ne mogu pojaviti u prirodi, postoji mnogo objekata koji izgledaju gotovo poput fraktala. Već smo vidjeli biljke, pahulje i obalu, a evo još nekoliko primjera:

Planinski lanac u središnjoj Aziji

Delta rijeke Ganges u Indiji

Vijci za munje

Krvne žile u mrežnici

Grand Canyon u SAD-u

Oblaci

Svi ti predmeti mogu se činiti potpuno slučajni, ali, baš kao i fraktali, postoji temeljni obrazac koji određuje kako su formirani. Matematika nam može pomoći da bolje razumijemo oblike, a fraktali imaju primjenu u područjima poput medicine, biologije, geologije i meteorologije.

Fraktalni teren generiran od računala

Fraktale možemo koristiti i za stvaranje realističnih „kopija“ prirode, na primjer, kao pejzaži i teksture koje se koriste u video igrama ili računalno generiranim filmovima. Vode, planine i oblake na ovoj slici u potpunosti je napravio računalo, uz pomoć fraktala!

A čak i možemo obrnuti ovaj postupak za komprimiranje digitalnih slika, kako bismo smanjili njihovu veličinu datoteke. Prve algoritme razvili su Michael Barnsley i Alan Sloan 1980-ih, a novi se i danas istražuju.

Promjena jezika

Prijavite se u Mathigon

Podijeli

Poništavanje napretka

Riječnik