FraktaliMandelbrotov set

Svi fraktali koje smo vidjeli u prethodnim poglavljima stvoreni su postupkom iteracije: započinjete s određenim uzorkom, a zatim ga ponavljate iznova i iznova.

To je slično drugom konceptu iz matematike koji ste vidjeli prije: s rekurzivnim nizovima, započinjete s određenim brojem, a zatim primjenjujete istu rekurzivnu formulu, iznova i iznova, kako biste dobili sljedeći broj u slijed.

Uzmimo kao primjer rekurzivnu formulu xn=xn−12 i crtajte njene pojmove na numeričkoj liniji. Možete promijeniti vrijednost x0:

Uočite kako se rezultirajući niz može ponašati vrlo različito, ovisno o početnoj vrijednosti x0:

Do sada nismo naučili ništa novo. Međutim, prije otprilike jednog stoljeća, matematičari su počeli istraživati što se događa s tim nizovima ako koristite složene brojeve, a ne samo pravi brojčani niz. Njihova otkrića bili su neki od najčudesnijih i najljepših rezultata u čitavoj matematici.

Julia Sets

Koristimo isti slijed kao prije, xn=xn−12, ali na složenoj ravnini. Možete pomaknuti položaj x0 da biste vidjeli što se događa sa sljedećim uvjetima. Ako slijed izgleda kao da se konvergira, obojite odgovarajuću točku na ravnini u plavu:

Kao što vidite, niz se konvergira sve dok x0 leži unutar jediničnog kruga outside the unit squareabove the >>>>x<<<<-axis (krug s polumjerom 1, centriran u izvoru).

Sada ćemo malo otežati stvari. Umjesto da samo usporedimo prethodni broj, svaki put dodamo i konstantnu c (što može biti bilo koji složen broj). Drugim riječima, xn=xn−12+c. Mislite li da ćemo ipak dobiti krug konvergencije? Koje biste još oblike mogli vidjeti? Nastaviti

U ovom dijagramu možete pomicati položaj x0 kao i vrijednost c:

Različiti oblici koji nastaju bojenjem u brojevima nazivaju se skupovi Julia. Dva francuska matematičara otkrila su samostalno, Gaston Julia i Pierre Fatou, oko 1918. godine.

U to vrijeme nije bilo računala koja bi mogla vizualizirati kako izgledaju Julijevi kompleti. Matematičari poput Julije i Fatou mogli su matematički rasuđivati o njima, ali samo su ikada vidjeli grube, ručno crtane skice onoga što bi mogli izgledati.

Danas nemamo ovaj problem - slike su dolje različite Julia. Različite boje govore kako se brzo redoslijed u toj točki razilazi:

Nastaviti

Mandelbrotov set

Prilikom stvaranja različitih Julia setova, mogli ste primijetiti da postoje neke vrijednosti c za koje se svaki niz razlikuje, a cijela složena ravnina ostaje bijela. Nekoliko desetljeća nakon Julije i Fatoua, nova generacija matematičara pokušala je preslikati kako ta područja izgledaju.

U prethodnom primjeru odabrali smo fiksnu vrijednost za c, a zatim promijenili položaj x0 u boji ravnine. Sada ispravimo vrijednost x0=0 i umjesto toga promijenimo vrijednost c.

Još jednom obojite preko složene ravnine da biste otkrili područje na kojem nizovi ostaju omeđeni. Koje oblike očekujete da se pojave?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Ovaj fraktal se zove Mandelbrot set, a kada se rotira za 90 °, izgleda gotovo kao osoba, glave, tijela i dvije ruke. Prvi put ga je definirao i nacrtao 1978. u istraživačkom radu matematičara Roberta Brooksa i Petera Matelskog:

Nekoliko godina kasnije, Benoit Mandelbrot koristio je moćna računala u IBM-u da bi stvorio mnogo detaljniju vizualizaciju fraktala, koji je kasnije dobio ime po njemu. Prvi ispisi izgledali su drugačije od očekivanih - sve dok nije shvatio da tehničari koji rade na pisačima čiste "nejasnost" oko ivice, pretpostavljajući da je to uzrokovano česticama prašine ili greškama pisača, a ne definirajuća karakteristika fraktala. ! Nastaviti

Kao i svi fraktalni materijali, Mandelbrot je zauvijek moguće "zumirati" pronalazeći nove obrasce u svim razmjerima. Ovdje možete zumirati dio Mandelbrotove garniture koja se zove dolina morskog konja. Crne točke su unutar Mandelbrotova skupa, gdje je niz ograničen. Obojene točke su izvan skupa Mandelbrot, gdje se niz razlikuje, a različite boje govore kako brzo raste do beskonačnosti:

Scale: ${pow(scale)}

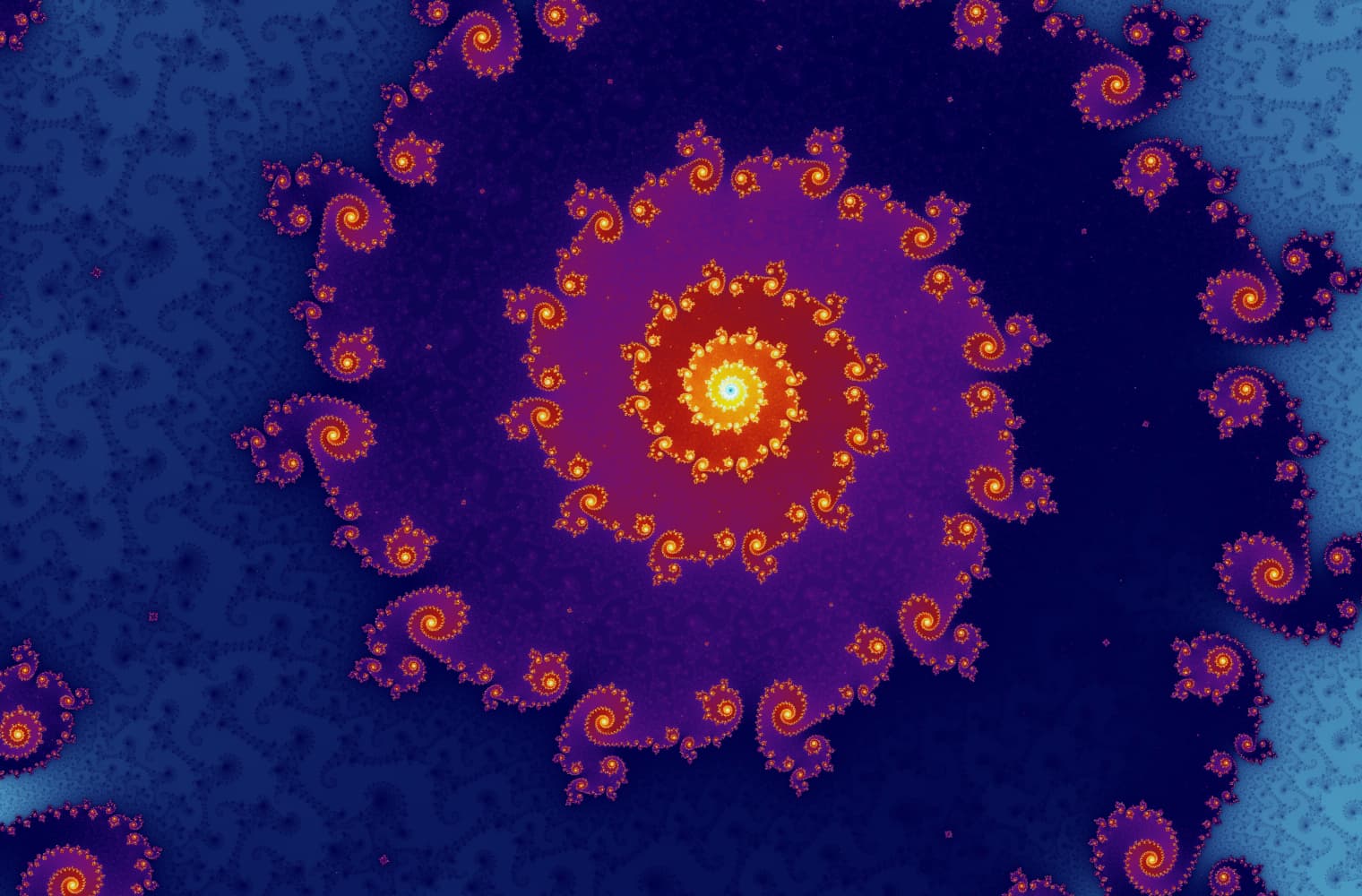
Ovaj se klizač sastoji od 27 pojedinačnih slika, do razine zumiranja veće od 14 kvadratnih milijardi, ili 254. Sve u svemu, trebalo im je gotovo 45 minuta da predstave moderni laptop. Mandelbrotov skup može se stvoriti samo jednom, jednostavnom jednadžbom, xn=xn−12+c, ali je beskrajno složen i zapanjujuće lijep.

Dok pomičete vrijednost c oko Mandelbrotovog skupa, možda ćete primijetiti znatiželjno svojstvo:

• Svi nizovi u glavnom tijelu Mandelbrotovog skupa konvergiraju sedivergereach an orbit u jednu točku.
• Sekvence unutar velike žarulje na vrhu dosežu orbituconvergediverge koja se sastoji od točaka.
• Sekvence u ovoj manjoj žarulji imaju orbite duljine .

Svaka žarulja ima orbitu različitog veličine, a manje žarulje imaju sve više i više točaka u svojoj orbiti. Veličina ovih orbita je usko povezana sa logističkom zemljovidom, važnim konceptom u teoriji haosa.