Poligoni i poliedritessellations

Poligoni se pojavljuju svuda u prirodi. Posebno su korisni ako želite obložiti veliku površinu, jer možete polirati poligone zajedno bez praznina ili preklapanja. Takvi se obrasci nazivaju tessellations .

Ljudi su kopirali mnoge od tih prirodnih obrazaca u umjetnosti, arhitekturi i tehnologiji - od antičkog Rima do danas. Evo nekoliko primjera:

Ovdje možete stvoriti vlastite tessellations koristeći pravilne poligone. Jednostavno povucite nove oblike s bočne trake na platno. Koji oblik tessellate dobro? Postoje li oblici koji se uopšte ne dišu? Pokušajte stvoriti zanimljive uzorke!

Examples of other students’ tessellations

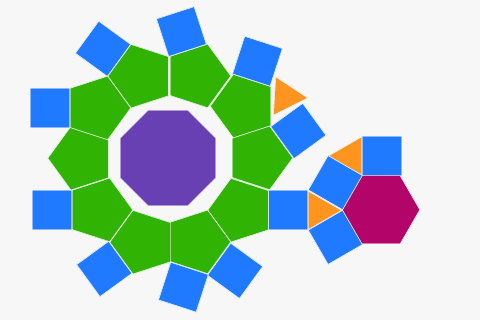
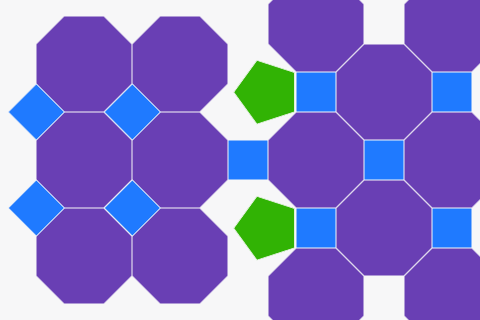
Tesselacije iz pravilnih poligona

Možda ste primijetili da postoje neki pravilni poligoni (poput kvadrata pentagoni ) tessellate vrlo lako, dok drugi (poput pentagona) trokuti šesterokutni ) uopće ne izgledaju tesno.

To ima veze s veličinom njihovih unutarnjih kutova , koje smo ranije naučili izračunati. U svakoj vrhovi teskele sastaju se unutarnji kutovi više različitih poligona. Sve ove kutove trebamo dodati do °, inače će doći do zazora ili preklapanja.

Isto tako možete provjeriti da se, poput pentagona, nijedan običan poligon sa 7 ili više strana ne tesi. To znači da su jedini pravilni poligoni koje tessellate trokut, kvadrat i šesterokut!

Naravno da možete kombinirati različite vrste pravilnih poligona u tessellaciji, pod uvjetom da se njihovi unutarnji kutovi mogu dodati i do 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Tesselacije s nepravilnih poligona

Također možemo pokušati napraviti tesselacije iz nepravilnih poligona - sve dok smo oprezni pri rotiranju i rasporedu.

Pentagoni su malo zamršeniji. Već smo vidjeli da se redoviti pentagoni ne sjede testenlat , ali što je s onima koji nisu normalni?

Evo tri različita primjera tessellation s pentagona. Nisu pravilni , ali savršeno vrijede 5-jednostrani poligoni.

Do sada su matematičari pronašli samo 15 različitih vrsta tessela s (konveksnim) pentagonima - od kojih je najnovija otkrivena u 2015. Nitko ne zna ima li drugih ili je tih 15 jedina ...

Tesselacije u čl

Tesselacije smo i alat i inspiracija mnogim umjetnicima, arhitektima i dizajnerima - najpoznatijim nizozemskim umjetnikom MC Escherom . Escherovo djelo sadrži čudna, mutirajuća stvorenja, obrasce i pejzaže:

Ova umjetnička djela često izgledaju zabavno i bez napora, ali osnovni matematički principi su isti kao i prije: kutovi, rotacije, prijevodi i poligoni. Ako matematika nije u redu, tesketa neće raditi!

“Metamorphosis II” by M. C. Escher (1940)

Peninove pločice

Sve tesselacije koje smo vidjeli do sada imaju jedno zajedničko: one su periodične . To znači da se sastoje od redovitog uzorka koji se ponavlja iznova i iznova. Oni mogu zauvijek nastaviti u svim smjerovima i izgledat će svugdje isto.

U 1970-ima je britanski matematičar i fizičar Roger Penrose otkrio neperiodične teshelacije - one i dalje traju beskonačno u svim smjerovima, ali nikada ne izgledaju potpuno isto. Zove se Penrose nagib , a za stvaranje jednog vam je potrebno samo nekoliko različitih vrsta poligona:

Penrose je istraživao tesselacije isključivo radi zabave, ali ispada da unutarnja struktura nekih stvarnih materijala (poput aluminija) slijedi sličan obrazac. Uzorak je čak korišten i na toaletnom papiru, jer su proizvođači primijetili da se neperiodični uzorak može namotati bez ispupčenja.