English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng ViệtPoligoni i poliedriPlatonske čvrste tvari
Na početku ovog tečaja definirali smo pravilan mnogokut je poligon u kojem su sve strane iste dužine, a svi unutarnji kutovi imaju istu veličinu.
U pravilnom poliedru sva su lica poliedra su poligoni koji čine njegovu površinu. "Uglovi" poliedra nazivaju se njegovi vrhovi. A Platonska krutina je višejednik gdje je svako lice pravilan mnogokut s istim brojem rubova i gdje se isti broj lica susreće u svakoj vrhovi. Postoji samo pet različitih platonskih krutih čestica: tetraedar, kocka, oktahedron, dodekahedron i ikosahedron. Platon (oko 425. - 347. pr.n.e.) bio je filozof u drevnoj Grčkoj, i - zajedno sa svojim učiteljem Sokratom i njegovim učenikom Aristotelom - postavio je sam temelj zapadne filozofije i znanosti. Platon je osnovao Atinsku akademiju, prvu visokoškolsku ustanovu u zapadnom svijetu. Njegova mnoga djela o filozofiji i teologiji, znanosti i matematici, politici i pravdi čine ga jednim od najutjecajnijih mislilaca svih vremena.
Pa kako izgledaju platonski kruti dijelovi - i koliko ih ima? Da bismo napravili trodimenzionalni oblik, potrebna su nam najmanje
Ako stvorimo poliedar u kojem se tri jednakostranični trokut je trokut u kojem sve tri strane imaju jednaku duljinu.
Ako se četiri jednakostranična trokuta susreću u svakoj vrhu, dobit ćemo različitu platonsku krutinu. Zove se Oktahedron i ima
Ako se
Ako se
A sedam ili više trokuta u svakoj verziji također ne stvaraju nove poliedre: nema dovoljno prostora oko vrha, da se uklopi u toliko trokut.
To znači da smo pronašli
Ako se
Ako se u svakom vrhu nalaze
Zatim pokušajmo s redovitim pentagonima:
Ako se
Kao i prije, četiri ili više pentagona
Sljedeći redovni poligon za pokušaj su šesterokutnici:
Ako se tri šesterokuta susreću u svakom vrhu, odmah dobivamo
Isto se događa i za sve redovne poligone s više od šest strana. Oni se ne sjedaju, a mi zasigurno ne dobivamo nikakve trodimenzionalne poligone.
To znači da postoji samo
Tetraedar
Kocka
oktaedar
dodekahedron
ikozaedra
Obavijest o tome kako je broj lica i vrhova su SVE
Polededar možemo pretvoriti u njegov dual, „zamjenom“ svakog lica s vrhom, i svakog vrha s licem. Ove animacije pokazuju kako:
Tetraedar je dvostruk sa sobom. Budući da ima isti broj lica i vrhova, njihovo mijenjanje ne bi ništa promijenilo.
Platon (oko 425. - 347. pr.n.e.) bio je filozof u drevnoj Grčkoj, i - zajedno sa svojim učiteljem Sokratom i njegovim učenikom Aristotelom - postavio je sam temelj zapadne filozofije i znanosti. Platon je osnovao Atinsku akademiju, prvu visokoškolsku ustanovu u zapadnom svijetu. Njegova mnoga djela o filozofiji i teologiji, znanosti i matematici, politici i pravdi čine ga jednim od najutjecajnijih mislilaca svih vremena.
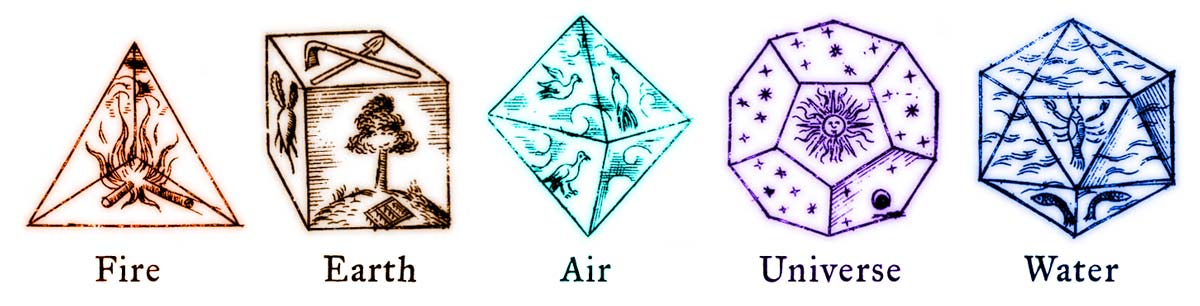
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)
Arhimedije
Platonske krute tvari posebno su važni poliedri, ali postoji bezbroj drugih.
Primjerice, Arhimedovo kruto tijelo je višejednik sastavljen od različitih vrsta pravilnih poligona, koji izgledaju iz svih smjerova isto. Postoji 13 različitih Arhimedovih krutina. pravilan mnogokut je poligon u kojem su sve strane iste dužine, a svi unutarnji kutovi imaju istu veličinu. Arhimed (oko 287. - 212. pr. Kr.) Bio je drevni grčki znanstvenik i inženjer i jedan od najvećih matematičara svih vremena. Otkrio je mnoge pojmove kalkulusa i radio u geometriji, analizi i mehanici. Dok se kupao, Arhimed je otkrio način da utvrdi volumen nepravilnih predmeta koristeći količinu vode koju su istisnuli prilikom potapanja. Bio je toliko uzbuđen ovim otkrićem da je istrčao na ulicu, još uvijek skinuta, vičući "Eureka!" (grčki za "Našao sam ga!"). Kao inženjer, izgradio je genijalne obrambene strojeve tijekom opsade svog rodnog grada Sirakuze na Siciliji. Nakon dvije godine, Rimljani su napokon uspjeli ući, a Arhimed je ubijen. Posljednje su mu bile riječi "Ne uznemiravaj moje krugove" - koje je tada proučavao.
Trnoviti tetraedar 8 lica, 12 vrhova, 18 rubova
Cuboctahedron 14 lica, 12 vrhova, 24 ruba
Trnovita kocka 14 lica, 24 vrhova, 36 rubova
Trnoviti oktahedron 14 lica, 24 vrhova, 36 rubova
Rhombicuboctahedron 26 lica, 24 vrhova, 48 rubova
Trnoviti kuboktaedar 26 lica, 48 vrhova, 72 ruba
Snub Cube 38 lica, 24 vrhova, 60 rubova
Icosidodecahedron 32 lica, 30 vrhova, 60 rubova
Skraćeni dodekahedron 32 lica, 60 vrhova, 90 rubova
Trnoviti ikozaedar 32 lica, 60 vrhova, 90 rubova
Rhombicosidodecahedron 62 lica, 60 vrhova, 120 rubova
Trnoviti ikozidodekahedron 62 lica, 120 vrhova, 180 rubova
Snub Dodekahedron 92 lica, 60 vrhova, 150 rubova
Prijave
Platon je pogrešno vjerovao da se svi elementi sastoje od platonskih krutih čestica. Ali obični poliedri imaju mnoga posebna svojstva zbog kojih se pojavljuju drugdje u prirodi - i ta svojstva možemo kopirati u znanost i inženjerstvo.
Radiolaria skeleton
Icosahedral virus
Mnogi virusi , bakterije i drugi mali organizmi imaju oblik Ikozaedar je platonska krutina i sastoji se od 20 lica koja su sve jednakostranični trokut. Ima 12 vrhova i 30 rubova.
Buckyball molecule
Montreal Biosphere
Mnoge su molekule oblikovane poput redovitih poliedra. Najpoznatiji primjer je Skraćeni ikozaedar je arhimedska krutina koja se sastoji od 12 pravilnih šesterokutova i 20 pravilnih šesterokutova.
Otkriven je 1985. kada su znanstvenici istraživali međuzvjezdanu prašinu. Nazvali su je "Buckyball" (ili Buckminsterfullerene) po arhitektu Richard Buckminster "Bucky" Fuller (1895. - 1983.) bio je američki arhitekt, dizajner i izumitelj. Poznat je po izgradnji geodetske kupole - velike, sferne građevine. Slične karbonske molekule, fullereni, kasnije su nazvane po njemu.
Fluorite octahedron
Pyrite cube
Većina kristala ima svoje atome raspoređene u pravilnoj mreži koja se sastoji od Tetrahedron je platonska krutina i sastoji se od četiri lica koja su jednakostranični trokut. Ima četiri vrha i šest rubova. Kocka(koja se ponekad naziva šesterokut) je pravilan višejednik u kojem je svako lice kvadrat. To je jedno od pet platonskih krutih čestica i ima 6 lica, 8 vrhova i 12 rubova. Oktahedron je platonska krutina i sastoji se od 8 lica koja su jednakostranični trokut. Ima 6 vrhova i 12 rubova.
Octagonal space frames
Louvre museum in Paris
Tetrahedri i oktaedri su nevjerojatno kruti i stabilni, što ih čini vrlo korisnim u gradnji . Svemirski okviri su poligonalne strukture koje mogu podupirati velike krovove i teške mostove.
Football
Polygonal role-playing dice
Platonske krute tvari također se koriste za stvaranje kockica . zbog svoje simetrije, svaka strana ima vjerojatnost je broj između 0 i 1 koji ukazuje na vjerojatnost nastanka određenog događaja. Vjerojatnost događaja A zapisuje se kao
Skraćeni ikozaedar je arhimedska krutina koja se sastoji od 12 pravilnih šesterokutova i 20 pravilnih šesterokutova. Skraćeni ikozaedar je arhimedska krutina koja se sastoji od 12 pravilnih šesterokutova i 20 pravilnih šesterokutova.