Nizovi i obrasciAritmetički i geometrijski niz

Godine 1682. astronom Edmond Halley opazio je neobičnu pojavu: blistavi bijeli objekt s dugačkim repom koji se kretao noćnim nebom. Bio je to komet, mala ledena stijena koja leti kroz svemir, ostavljajući iza sebe trag prašine i leda.

Halley se sjetio da su i drugi astronomi primijetili slične komete mnogo ranije: jedan 1530., a drugi 1606. Primijetite da je vremenski razmak između dva uzastopna opažanja u oba slučaja jednak: godina.

Image of Halley’s Comet,
taken in 1986 on Easter Island

Halley je zaključio da su sva tri opažanja zapravo isti komet - koji se danas naziva Halleyev komet. Orbitira oko sunca i prolazi uz Zemlju otprilike svakih 76 godina. Također je predvidio kada će komet biti vidljiv sljedeći put:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

Zapravo, vremenski interval nije uvijek točno 76 godina: može varirati za jednu ili dvije godine, jer na orbitu kometa utječu drugi planeti. Danas znamo da su Halleyev komet promatrali stari astronomi već 240. godine prije Krista!

Depections of Halley’s comet throughout time: a Babylonian tablet (164 BC), a medival tapestry (1070s), a science magazine (1910) and a Soviet stamp (1986).

Druga skupina znanstvenika istražila je ponašanje teniske loptice koja odskakuje. Bacili su loptu s visine od 10 metara i tijekom vremena izmjerili njen položaj. Svakim odbijanjem lopta gubi dio svoje izvorne visine:

Znanstvenici su primijetili da lopta gubi 20% svoje visine nakon svakog odbijanja. Drugim riječima, maksimalna visina svakog odskoka je 80% od prethodnog. To im je omogućilo predviđanje visine svakog sljedećeg odskoka:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Definicije

Ako uspoređujemo oba ova problema, primijećujemo da postoje mnoge sličnosti: niz Halleyevog kometa ima istu između uzastopnih elemenata niza, dok redoslijed odskoka za tenisku lopticu ima isti između uzastopnih elemenata niza.

Nizovi s tim svojstvima imaju posebno ime:

Aritmetički niz ima konstantnu razliku d između uzastopnih elemenata niza.

Isti se broj dodaje ili oduzima svakom elementu, da bi se dobio sljedeći.

Geometrijski niz ima konstantan kvocijent r dvaju uzastopnih elemenata niza.

Svaki se element množi ili dijeli s istim brojem, da bi se dobio sljedeći.

Evo nekoliko različitih nizova. Možete li odrediti koji su aritmetički, geometrijski ili ni jedan ni drugi, i koje su vrijednosti d i r?

2, 4, 8, 16, 32, 64, ...

je _{span.reveal(when="blank-0")}, s kvocijentom .

2, 5, 8, 11, 14, 17, ...

je , s razlikom

17, 13, 9, 5, 1, –3, ...

je , s razlikom .

2, 4, 7, 11, 16, 22, ...

nije .

40, 20, 10, 5, 2,5, 1,25, ...

je _{span.reveal(when="blank-7")}, s omjerom .

Da bismo definirali aritmetički ili geometrijski niz, moramo znati ne samo razliku ili kvocijent, već i početnu vrijednost (zvanu a). Ovdje možete generirati vlastite nizove i crtati njihove vrijednosti na grafikonu, mijenjajući vrijednosti a, d i r. Možete li pronaći neki uzorak?

Aritmetički niz

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Geometrijski niz

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Primjetite kako svi aritmetički nizovi izgledaju vrlo slično: ako je razlika pozitivna, oni konstantno , a ako je razlika negativna, oni konstantno .

Geometrijski nizovi, s druge strane, mogu se ponašati potpuno drugačije ovisno o vrijednosti a i r:

Ako je r>1, elementi , sve do beskonačnosti. Matematičari kažu da niz divergira

Ako je r između -1 i 1, elementi će uvijek . Kažemo da niz konvergira

Ako je r<−1 elementi niza izmjenjuju se između pozitivnih i negativnih, dok njihova postaje veća.

Saznajte više o konvergenciji i divergenciji u posljednjem odjeljku ove teme.

Rekurzivne i eksplicitne formule

U prethodnom smo poglavlju naučili da se rekurzivnom formulom određuje vrijednost svakog elementa niza kao funkcija prethodnih elemenata. Ovo su rekurzivne formule za aritmetički i geometrijski niz:

xn=

Jedan problem s rekurzivnom formulom je da, na primjer, da bismo pronašli 100. element, prvo moramo izračunati prethodnih 99 elemenata - a to bi moglo potrajati dugo. Umjesto toga, možemo pokušati pronaći eksplicitnu formulu kojom izravno određujemo vrijednost n-tog elementa.

Za aritmetičke nizove, moramo dodati d pri svakom koraku:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

Na n-tom elementu niza dodajemo puta d, tako da je opća formula

xn=a+d×n−1.

Za geometrijske nizove, moramo pomnožiti s r pri svakom koraku:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

Za n-ti element množimo puta r, tako da je opća formula

xn=a×rn−1.

Ovdje je sažetak svih definicija i formula koje ste dosad vidjeli:

Aritmetički niz ima prvi element a i istu razliku d između uzastopnih elemenata niza.

Rekurzivna formula: xn=xn−1+d

Eksplicitna formula: xn=a+d×n−1

Geometrijski niz ima prvi element a i isti kvocijent r između uzastopnih elemenata niza.

Rekurzivna formula: xn=xn−1×r

Eksplicitna formula: xn=a×rn−1

Pogledajmo nekoliko primjera gdje sve to možemo upotrijebiti!

Šalji dalje

Evo kratkog isječka iz filma Šalji dalje, gdje 12-godišnji Trevor objašnjava svoju ideju kako učiniti svijet boljim mjestom:

Suština Trevorove ideje je da, ako svi "šalju dalje", jedna osoba može imati ogroman utjecaj na svijet:

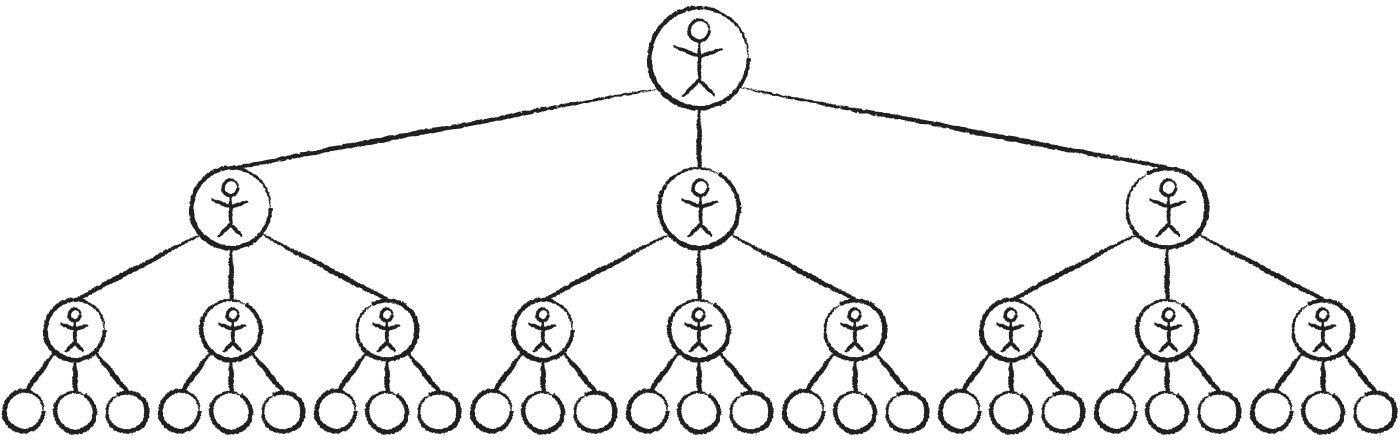
Primijetite kako broj ljudi na svakom koraku čini , sa stalnim kvocijentom :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Pomoću eksplicitne formule za geometrijski niz, možemo utvrditi koliko je novih ljudi zahvaćeno u bilo kojem koraku:

xn =

Broj ljudi se nevjerojatno brzo povećava. U 10. koraku zahvatili biste 19.683 novih, a nakon 22 koraka zahvatili biste više ljudi nego što trenutno živi na Zemlji.

Ovaj niz brojeva ima posebno ime: potencija od 3. Kao što vidite, svaki je element neka potencija od 3:

30, 31, 32, 33, 34, 35, …

Tko želi biti milijunaš?

Uskoro!

Problem sa šahovskom pločom

Uskoro!

Promjena jezika

Prijavite se u Mathigon

Podijeli

Poništavanje napretka

Riječnik