Nizovi i obrasciFibonaccijevi brojevi

Zamislite da ste dobili par mladih zečeva, jednog mužjaka i jednu ženku. Oni su vrlo posebni zečevi, jer nikada ne umiru, a ženka rađa novi par zečeva točno jednom mjesečno (uvijek novi par mužjaka i ženki).

U prvom mjesecu, zečevi su jako mali i ništa se ne događa – ali oni jako brzo rastu.

Nakon mjesec dana, zečevi su odrasli i mogu se početi razmnožavati…

… i nakon još mjesec dana, dobit će svoj prvi par podmlatka. Sada imate dva para zečeva.

U sljedećem mjesecu, vaš par zečeva dobit će još jedan par podmlatka. U međuvremenu, prvi par djece je odrastao. Sada imate ukupno tri para.

U petom mjesecu, vaš prvi par dobit će još jedan par podmlatka. U isto vrijeme, njihov prvi podmladak je sad dovoljno star da dobije prve unuke početnog para. Sada imate pet parova zečeva.

U šestom mjesecu, još tri para dobit će podmladak: početni par i njihova prva dva para djece.

U sljedećem mjesecu imali biste 13 parova zečeva: 8 iz prethodnog mjeseca, plus 5 novih beba. Možete li otkriti uzorak u ovom nizu?

Broj zečeva u određenom mjesecu je . Drugim riječima, trebate dodati prethodna dva elementa niza da biste dobili sljedeći. Niz započinje s dvije jedinice, a rekurzivna formula je_

xn = xn−1 + xn−2

Možete li izračunati broj zečeva nakon još nekoliko mjeseci?

1, 1, 2, 3, 5, 8, , , , , , , …

Dakle nakon 12 mjeseci imate 144 para zečeva!

Taj niz brojeva zove se Fibonaccijev niz, nazvan po talijanskom matematičaru Leonardu Fibonacciju.

Kada se Fibonacci rodio 1175. godine, većina ljudi u Europi još uvijek je koristila rimske brojke za zapis brojeva (npr. IVX ili MCMLIV). Fibonacijev otac bio je trgovac i zajedno su putovali u sjevernu Afriku, kao i na Bliski Istok. Tamo je Fibonacci prvi naučio koristiti arapske brojke.

Kada se vratio u Italiju, Fibonacci je napisao knjigu naziva Liber Abaci (latinski za "Knjiga o računanju"), gdje je prvi uveo nove arapske brojke europskim trgovcima. Oni su bili trenutan uspjeh - i danas ih koristimo.

Portrait of Leonardo Fibonacci

Na jednoj od stranica u svojoj knjizi, također je istraživao uzgojne obrasce zečeva - zato su Fibonaccijevi brojevi nazvani po njemu.

Pages from Fibonacci’s Liber Abaci

Naravno, Fibonaccijevi brojevi ne opisuju način na koji se zečevi razmnožavaju u stvarnom životu. Kunići nemaju točno jednog muškog i jednog ženskog potomka svaki mjesec, a nije uračunato ni da će kunići na kraju i umrijeti.

Ipak, čini se da u prirodi postoje mnoga druga mjesta na kojima se pojavljuju Fibonaccijevi brojevi; na primjer spirale u biljkama. Možete li prebrojati koliko spirala ima u svakom smjeru?

Original

U smjeru kazaljki na satu

Suprotno od kazaljki na satu

Ovaj češer ima spirala u smjeru kazaljke na satu i spirala u smjeru suprotnom od smjera kazaljke na satu.

Original

U smjeru kazaljki na satu

Suprotno od kazaljki na satu

Ovaj suncokret ima 34 spirale u smjeru kazaljke na satu i 55 spirala u smjeru suprotnom od smjera kazaljke na satu.

U oba slučaja brojevi spirala su uzastopni Fibonaccijevi brojevi. Isto vrijedi i za mnoge druge biljke: sljedeći put kad izađete van, brojite latice u cvijetu ili broj listova na stabljici. Vrlo često ćete otkriti da su to Fibonaccijevi brojevi!

Naravno, to nije samo slučajnost. Postoji važan razlog zbog kojeg priroda voli Fibonaccijev niz, o kojem ćete saznati više kasnije.

Mužjaci

Ženke

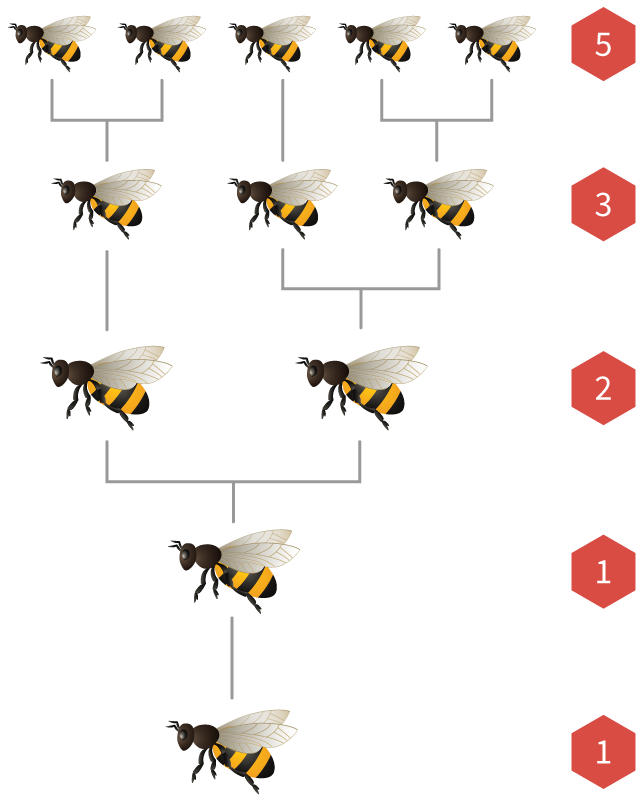
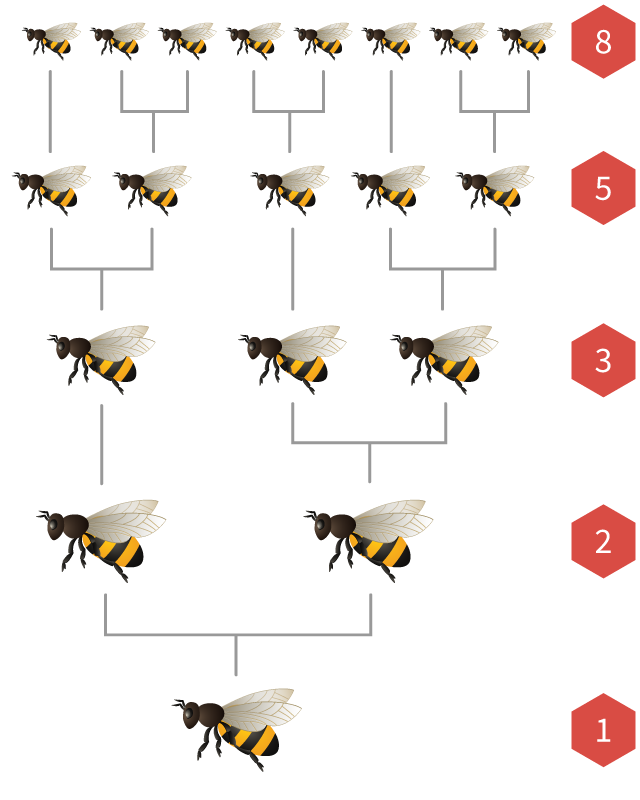
Fibonaccijevi brojevi pojavljuju se i u populacijama pčela.

U svakoj koloniji pčela postoji po jedna kraljica koja polaže mnogo jaja. Ako jaje oplodi muška pčela, ono se izleže u žensku pčelu. Ako nije oplođeno, izleže se u mušku pčelu (zvanu radilica).

To znači da ženske pčele imaju , dok muške pčele imaju samo .

Ako nacrtamo pčelinje obiteljsko stablo, brojevi roditelja, baka i djedova, pradjedova i ranijih generacija uvijek će biti Fibonaccijevi brojevi!

Povremeno se mlade pčele hrane posebnom hranom koja se zove "matična mliječ". U tom se slučaju pretvaraju u kraljice i odletjet će van kako bi osnovale novu košnicu.

Zlatni rez

Baš kao trokutni i kvadratni brojevi i još neki nizovi koje smo vidjeli prije, Fibonaccijev niz može se prikazati pomoću geometrijskog uzorka:

Počinjemo s dva kvadratića veličine 1.

Dalje, dodajemo novi kvadrat veličine 2, formirajući veći pravokutnik.

Dalje, dodajemo kvadrat veličine 3, formirajući još veći pravokutnik.

Sljedeći kvadrat ima veličinu 5. Primjećujete li da stvaramo Fibonaccijeve brojeve?

Ako nastavimo dodavati kvadrate, oni će biti veličine 8, 13, 21, i tako dalje.

Možda ste primjetili da, kako se pravokutnici povećavaju, čini se da počinju formirati spiralu. Ovo možemo vizualizirati tako da nacrtamo pravilnu spiralu koja povezuje kutove kvadrata.

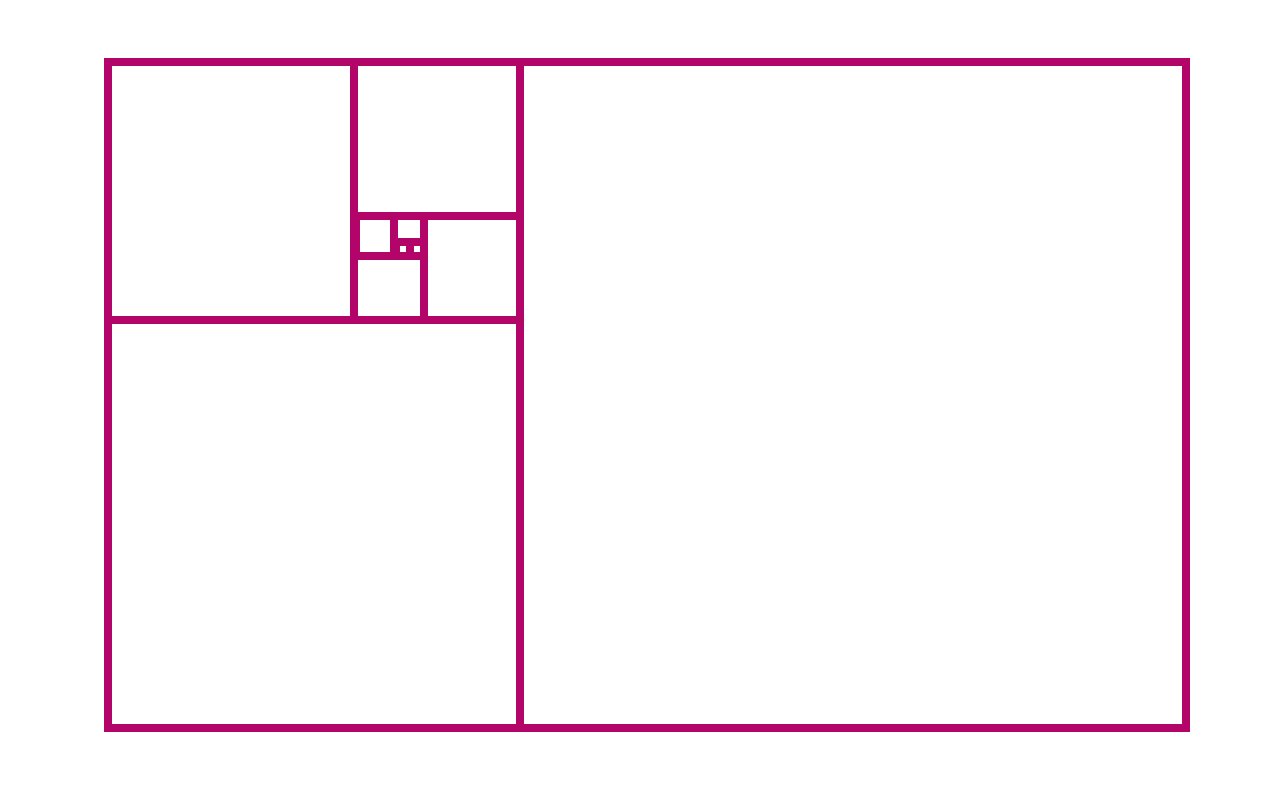
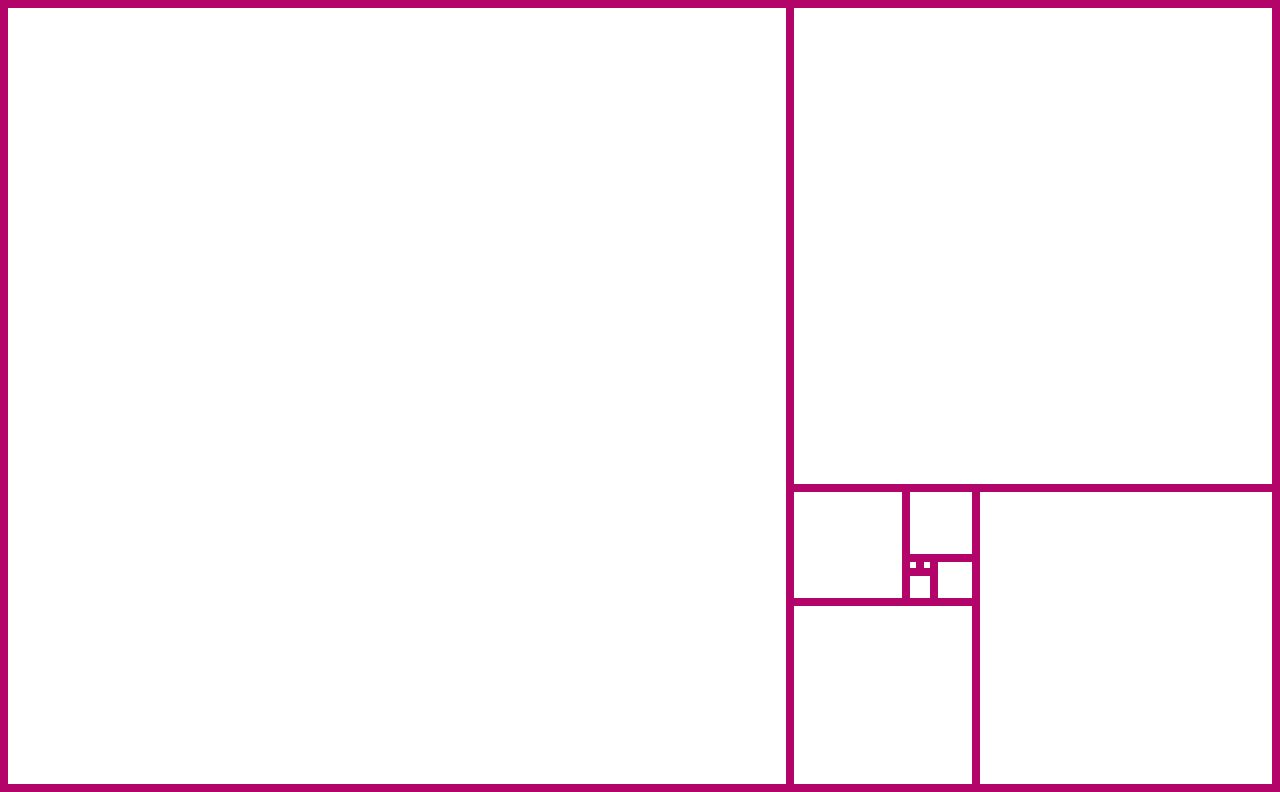
Na svakom koraku, kvadrati formiraju veći pravokutnik. Njegova širina i visina uvijek su dva uzastopna Fibonaccijeva broja. Format pravokutnika je omjer njegove širine i njegove duljine:

21 = 2

32 = 1.5

53 = 1.666 ...

85 = 1.6

= 1.625

= 1.62…

Primijetite kako se, dodajući sve više i više kvadrata, čini da se omjer slike približava određenom broju oko 1,6. Ovaj se broj zove zlatni rez i obično je predstavljen grčkim slovom φ ("phi"). Točna je njegova vrijednost

1+52=1.61803398875…

Mnogi vjeruju da zlatni rez ima posebnu estetsku vrijednost. Zato ga često koriste umjetnici i arhitekti - kao u ova dva primjera:

Vjeruje se da je grčki kipar Fidija koristio zlatni rez pri dizajnu Partenona u Ateni. Prvo slovo njegova imena, φ, simbol je koji se koristi za zlatni rez.

Sakrament Posljednje večere, španjolskog umjetnika Salvadora Dalíja, jedna je od mnogih slika u zlatnom rezu. U pozadini se također može vidjeti veliki dodekaedar.

Zlatni rez možemo aproksimirati dva uzastopna Fibonaccijeva broja.

Međutim, ispada da se točna vrednost φ ne može zapisati kao jednostavan razlomak: to je iracionalni broj, baš kao π i 2 i neki drugi brojevi koje ste vidjeli prije.

Fibonaccijeva spirala

Zlatni rez objašnjava zašto se Fibonaccijevi brojevi pojavljuju u prirodi, poput suncokreta i češera koje ste vidjeli na početku ovog poglavlja.

Obje ove biljke rastu prema van iz svojeg središta (dio biljke nazvan meristem). Kako izrastaju nove sjemenke, lišće ili latice, one guraju postojeće dalje prema van.

Pomaknite klizač desno da biste vidjeli kako biljka raste. Uočite kako se svaki list dodaje drugačijom rotacijom od prethodnog. Kut između dva uzastopna lista uvijek je isti.

Za cvijeće je važan odgovarajući kut: lišće i sjemenke moraju biti približno jednako raspoređeni kako bi dobili najveću količinu sunčeve svjetlosti i hranjivih sastojaka. Na donjem dijagramu možete istražiti kako može izgledati suncokret s različitim kutovima između njegovih sjemenki:

Ako je kut 0 °, sve će sjemenke rasti u jednom dugom redu daleko od središta.

Ako je kut 12 punog okretaja (180 °), sjemenke će se izmjenjivati između dva odvojena "kraka" koji se odmiču od središta.

Ako je rotacija neki drugi udio od 360 °, na primjer 25 ili 13 ili 38, tada će broj "krakova" biti isti kao i tog razlomka.

Nažalost, "ruke" su loše, jer znače da sjeme nije ravnomjerno raspoređeno: sav je prostor između krakova izgubljen. Ali ako racionalni brojevi ne odgovaraju, pokušajmo iracionalne brojeve!

Jedan primjer iracionalnog broja je π. Ali ako je kut između sjemenki 1π 360 °, i dalje imamo oružje: njih 22. To je zato što je razlomak 227=3.1429… prilično dobra aproksimacija za π. Ono što nam stvarno treba je iracionalni broj koji se ne može aproksimirati jednostavnim razlomkom.

Čini se da je zlatni rez upravo to: "najracionalniji" od svih iracionalnih brojeva. Ako je kut između sjemena 1φ 360 °, ono izgleda gotovo savršeno raspoređeno. A upravo je to kut koji koriste biljke širom svijeta.

Sjetite se od prije da se omjeri uzastopnih Fibonaccijevih brojeva sve više približavaju zlatnom rezu - i zato ćete, ako brojite spirale u biljci, često pronaći Fibonaccijev broj.

Važno je zapamtiti da priroda ne zna za Fibonaccijeve brojeve. Priroda također ne može riješiti jednadžbe za izračun zlatnog reza - ali tijekom milijuna godina, biljke su imale dovoljno vremena da isprobaju različite pristupe i otkriju koji je najbolji.

Biljke i životinje uvijek žele rasti na najučinkovitiji način i upravo zato je priroda puna pravilnih, matematičkih obrazaca.

Fibonachos

Do sada smo za Fibonaccijeve brojeve koristili samo rekurzivnu formulu. Zapravo postoji i eksplicitna jednadžba - ali nju je mnogo teže pronaći:

Fn=151+52n−1−52n

Također bismo mogli pokušati odabrati različite početne točke za Fibonaccijeve brojeve. Na primjer, ako krenemo s 2, 1, ... a ne s 1, 1, ... dobit ćemo niz nazvan Lucasovi brojevi.

Ispada da, bez obzira koja dva početna broja odaberete, rezultirajući nizovi imaju mnoga ista svojstva. Na primjer, omjeri uzastopnih elemenata niza uvijek će konvergirati u zlatni rez.

${a}, ${b}, ${a+b}<<<<, ${a+2×b}<<<<, ${2×a+3×b}<<<<, ${3×a+5×b}<<<< , ${5×a+8×b}<<<<, ${8×a+13×b}<<<<, ...

Postoje mnoge zagonetke, obrasci i aplikacije povezane s Fibonaccijevim brojevima. Evo nekoliko primjera koje možete i sami isprobati:

Rješavanje problema

1. Fibonacijeva djeljivost

(a) Koji su Fibonaccijevi brojevi parni? Postoji li uzorak po kojem znamo redni broj elementa niza? Možete li objasniti zašto?

(b) Koji su Fibonaccijevi brojevi djeljivi s 3 (ili djeljivi s 4)? Što primjećujete?

2. Fibonaccijevi zbrojevi

Što se događa ako zbrojite bilo koja tri uzastopna Fibonaccijeva broja? Možete li objasniti zašto?

3. Fibonaccijeva stubišta

Kad hodamo stepenicama, možemo stati na svaku stepenicu ili preskakati dvije stepenice odjednom. To znači da postoji mnogo različitih mogućnosti za penjanje stepenicama. Na primjer, ako postoji 5 stepenica, imamo 8 različitih izbora:

Koliko izbora ima za stubište sa 6, 7 ili 8 stepenica? Možete li otkriti uzorak? I kako je to povezano s Fibonaccijevim brojevima?

Promjena jezika

Prijavite se u Mathigon

Podijeli

Poništavanje napretka

Riječnik

Nizovi i obrasciFibonaccijevi brojevi

Zlatni rez

Fibonaccijeva spirala

Fibonachos

Rješavanje problema