Preslikavanja i simetrijaGrupe simetrija i pozadine
Neki likovi imaju više od jedne simetrije - pogledajmo








Već ste zaključili da kvadrat ima
Također je i centralno simetričan za
I na kraju, možemo razmišljati i na način da je "ne raditi ništa" posebna vrsta simetrije - jer je rezultat (očito) isti kao na početku. Ovo se ponekad naziva identitet.
Ukupno smo pronašli
Sada možemo početi računati s ovim simetrijama. Na primjer, možemo dodati dvije simetrije kako bismo dobili nove:






Kad god zbrojimo dvije simetrije kvadrata, rezultat je nova simetrija. Ovo je "kalkulator simetrije", gdje to možete i sami isprobati:
Provedite malo vremena igrajući se s kalkulatorom simetrije i pokušajte pronaći neki obrazac. Možete li dopuniti ova zapažanja?
- Zbrajanje dviju rotacija uvijek daje
(ili identitet). - Zvrajanje dviju refleksija uvijek daje
(ili identitet). - Zbrajanje dviju istih simetrija u suprotnom redoslijedu
rezultat. - Zbrajanje identiteta
.
Možda ste primjetili da je zbrajanje simetrija zapravo vrlo slično zbrajanju cijelih brojeva:
- Zbrajanje dviju simetrija/cijelih brojeva uvijek daje novu simetriju/cijeli broj:
+ = 12 + 7 = 19 - Zbrajanje simetrija/cijelih brojeva je
asocijativno :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Svaka simetrija/cijeli broj ima inverz, drugu simetriju/cijeli broj koji, kad zbrajamo s njim, daje identitet:
+ = 4 + –4 = 0
U matematici, svaki skup koja ima ta svojstva zove se
Na primjer, grupe simetrija različitih molekula mogu znanstvenicima pomoći predvidjeti i objasniti svojstva nekih materijala. Grupe se također mogu koristiti za analizu pobjedničke strategije u društvenim igrama, ponašanja virusa u medicini, različitih harmonija u glazbi i mnogih drugih koncepata ...
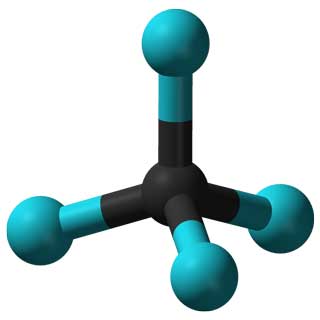
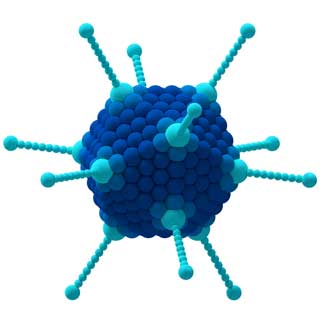
Svojstva molekule CCl 4 (lijevo) i Adenovirusa (desno) određena su njihovim simetrijama.
Popoločavanja ravnine
U prethodnim odjeljcima vidjeli smo dvije različite vrste simetrija kojima odgovaraju dvije različite transformacije: rotacije i refleksije. Ali postoji i simetrija za treću vrstu transformacije u ravnini:


Šesterokutne saće


Keramičke zidne pločice
Osim translacije, osne i centralne simetrije, postoji čak i četvrta vrsta:


Uzorak može imati više vrsta simetrije. Kao i kod kvadrata, možemo pronaći
Ove grupe ne govore mnogo o tome kako izgleda uzorak <<<< (npr. njegovu boju i oblik), nego samo kako se ponavlja <<<<. Više različitih uzoraka može imati istu grupu simetrija - sve dok su raspoređeni i ponavljaju se na isti način.


Ova dva uzorka imaju iste simetrije, iako izgledaju posve različito. Ali simetrije se ni ne bave bojama ili oblicima na površini.


Ova dva uzorka također imaju iste simetrije - iako izgledaju sličnije odgovarajućim uzorcima na lijevoj strani, nego jedni drugima.
Iako postoji beskonačno mnogo mogućih uzoraka, svi oni pripadaju jednoj od samo 17 različitih grupa simetrija. Te grupe zovu se popločavanja ravnine. Svako popločavanje ravnine definirano je kombinacijom translacija, rotacija, osnih simetrija i kliznih zrcaljenja. Možete li vidjeti

Group 1 – P1
Only translations

Group 2 – P2
Rotations of order 2, translations

Group 3 – P3
Rotations of order 3 (120°), translations

Group 4 – P4
Four rotations of order 2 (180°), translations

Group 5 – P6
Rotations of order 2, 3 and 6 (60°), translations

Group 6 – PM
Parallel axes of reflection, translations

Group 7 – PMM
Perpendicular reflections, rotations of order 2, translations

Group 8 – P4M
Rotations (ord 2 + 4), reflections, glide reflections, translations

Group 9 – P6M
Rotations (ord 2 + 6), reflections, glide reflections, translations

Group 10 – P3M1
Rotations of order 3, reflections, glide reflections, translations

Group 11 – P31M
Rotations of order 3, reflections, glide reflections, translations

Group 12 – P4G
Rotations (ord 2 + 4), reflections, glide reflections, translations

Group 13 – CMM
Perpendicular reflections, rotations of order 2, translations

Group 14 – PMG
Reflections, glide reflections, rotations of order 2, translations

Group 15 – PG
Parallel glide reflections, translations

Group 16 – CM
Reflections, glide reflections, translations

Group 17 – PGG
Perpendicular glide reflections, rotations of order 2, translations
Nažalost, ne postoji jednostavan razlog zašto ovih grupa ima točno 17, a dokazivanje toga zahtijeva provodi se pomoću naprednije matematike. Umjesto toga, pokušajte nacrtati vlastite ponovljene uzorke za svaku od 17 popločavanja ravnine:
Primjeri crteža drugih učenika



Popločavanja ravnine odnose se na ravne, dvodimenzionalne uzorke. Za trodimenzionalne uzorke možemo učiniti nešto slično: radi se o grupama kristala, a ima ih 219!
Osim translacija, refleksija, rotacija i kliznih zrcaljenja, ove grupe uključuju simetrije poput klizanja ravnine i zavijanja osi (usporedite s pokretom prilikom odvrtanja čepa na boci).
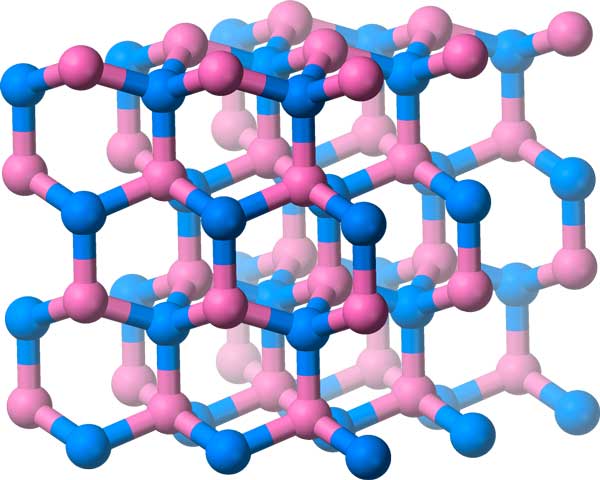
Molekule bor-nitrida raspoređene su u ovoj kristalnoj rešetki koja ima trodimenzionalnu grupu simetrija.